Prony’s Method
N complex data samples x [1], x [2] … x [N]
The Prony Method will estimate x [N] with p-term exponential model.
![]() (1)
(1)
for 1 ≤ n ≤ N, where T is the sample interval in seconds, Ak is the amplitude of the complex exponential, αk is the damping factor.
In real data samples,
![]() (2)
(2)
Original Prony Concept
![]() (3)
(3)
We used exactly 2p complex samples x [1], x [2], … x [p] to model 2p complex parameters h1, h2, h3 … hp; z1, z2, z3 … zp.
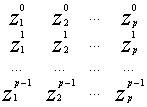 *
* ![]() =
= ![]() (4)
(4)
If we obtain a method to determine the z elements separately, the eq. (4) represents a set of linear simultaneous equations that can be solved for the unknown vector of complex amplitudes. Prony’s contribution was the discovery of such a method.
In order to find the form of this difference equation, first define the polynomial Ř (z) that has the zk exponents as its roots,
Ř (z) = ![]() (5)
(5)
If the products of eq. (5) are expanded into a power series, then the polynomial may be represented as
Ř (z) = ![]() = a [0]zp + a[1]zp-1 + … + a[p]z0 (6)
= a [0]zp + a[1]zp-1 + … + a[p]z0 (6)
with complex coefficients a [m] such that a [0] = 1. Shifting the index on eq. (3) from n to n-m and multiplying by the parameter a [m] yields
a [m]x[n-m] = ![]() (7)
(7)
Forming similar products a [0] x [n], … a [m-1]x [n-m+1] and summing produces
![]() (8a)
(8a)
![]() p+1 ≤
n ≤ 2p (8b)
p+1 ≤
n ≤ 2p (8b)
The right-hand sight of summation in eq. (8b) may be recognized as the polynomial defined by eq. (6), evaluated at each of roots zi, yielding the zero result indicated. Equation (8b) is the linear difference equation whose homogeneous solution is given by eq. (3). The polynomial is the characteristic equation associated with this linear difference equation.
a [1]x [p] + a [2]x [p-1] + … + a [p]x[1] = -x[p+1] (8c)
The p equations representing the valid values of a[n] that satisfy eq. (8b) may be expressed as the pxp matrix equation
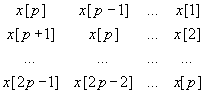 *
* ![]() =
= 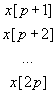 (9)
(9)
The damping αi and sinusoidal frequency fi may be determined from the root zi using the relationship.
αi = In |zi| / T sec-1 (10)
fi
= tan-1 [Im{zi} / Re {zi}] Hz (11)
The Prony procedure to fit p exponentials to 2p complex data samples may be now be summarized in three steps. First solution of equation (9) for the polynomial coefficients is obtained. Second, the roots of the polynomial defined by eq. (6) are calculated. The damping αi and sinusoidal frequency fi may be determined from the roots using the relationship (10) and (11). At the third step, we used the computed roots to construct the matrix elements of eq. (4). The amplitude Ai and the initial phase θi may be determined from each hi parameter with the relationships
Ai = |hi| (12a)
θi = tan-1 [Im {hi} / Re {hi}] radians (12b)
Matrix Pencil Method
In general, the signal model of the observed late time of electromagnetic-scattered-energy response from an object can be represented as
y (t) = x (t) + ε
(t) ≈ ![]() Ri esi t + ε (t) 0 ≤ t ≤ T (1)
Ri esi t + ε (t) 0 ≤ t ≤ T (1)
y (t) : observed time response
ε (t) : noise in the system
x (t) : signal
Ri : residues or complex amplitudes
si = -αi + j wi
α : damping factor
wi : angular frequencies (wi = 2Πfi)
After sampling the time variable, t, is replaced by kTs where Ts is the sampling period. The sequence can be written as
y (kTs) = x (kTs)
+ ε (kTs) ≈ ![]() Ri zki + ε (kTs) for k = 0, … , N-1 (2a)
Ri zki + ε (kTs) for k = 0, … , N-1 (2a)
And
Zi = exp(siTs) = exp(-αi + j wi)Ts for I = 1,2, … ,M (2b)
The target is to find the best estimates of M, Ri’s and zis from the noise-contaminated data, y(kTs). In general, simultaneous estimation of M, Ri’s and zis is a nonlinear problem.
Pencil term arises when combining two functions defined on a common interval, with scalar parameter, λ:
f(t, λ) = g(t) + λh(t) (3)
f(t, λ) is called a pencil of functions g (t) and h(t), parameterized by λ. To avoid obvious triviality, g(t) is not permitted to be scalar multiple of h(t).
Generalized Pencil of
Function Method
Assume that samples of any signal (yk) can be described by:
![]()
Where k=0,1, ... , N-1, bi are the complex residues, si are the complex poles, and dt is the sampling interval. For notational brevity, we can let zi = exp(sidt) which are the poles in the Z plane. It is clear that bi and si should respectively be in complex conjugate pairs for real values of yk .
Following the idea of the pencil-function method, we consider the following set of information vectors :
y0, y1, y2,..., yL
(2)
where
yi = [yi
, yi+1 ,..., yi+N-L] T (3)
The superscript T denotes the transpose of a matrıx. Based on these vectors, we define the matrices Y1 and Y2 as follows:
Y1 = [yo , y1
,..., yL-1] (4)
Y2 = [y1 , y2
,..., yL] (5)
To look into the underlying structure of the two matrices, one can write
Y1 = Z1 B Z2 (6)
Z1 = Z1 B Z0Z2 (7)
where
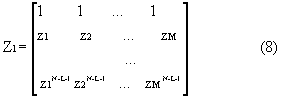

Z0 = diag(z1 , z2 , ... , zM) (10)
B = diag(b1 , b2 , ... , bM) (11)
Based on the above decomposition of Y1 and Y2 , one can show that if M<L<N-M the poles {zi ; i =1,...,M} are the eigen values of the matrix pencil Y2 - z Y1 . To develop and illustrate the use of an algorithm for computing the generalized eigen values of the matrix-pencil problem we can write
Y1 + Y2 =
Z2 + B –1 Z1 + Z1
B Z0Z2
= Z2 + Z0Z2 (12)
where the superscript + denotes the Moore-Penrose pseudo-inversewhereas we use –1 for the regular inverse. It can be seen from (12) that there exist vectors {pi ; i =1,...,M} such that
Y1 + Y1 pi = pi (13)
and
Y1 + Y2 pi = zi pi (14)
The pi are called the generalized eigen vectors of Y2 - z Y1. To compute the pseudo-inverse Y1 + one can use the singular value decomposition (SVD) of Y1 as follows:
![]()
![]()
where U = [u1 , u2 ,..., uM] , V = [v1 , v2 ,..., vM] and D = diag(d1 , d2 , ... , dM). The superscript H denotes the conjugate trasnpose of a matrix. U and V are matrices of left and right singular vectors, respectively. Note that for noisy data or to decide how many exponentials are to be used in the algorithm one should choose d1 , d2 , ... , dM to be the M largest singular values of Y1 and the resulting Y1 + is called the truncated pseudo-inverse of Y1 . Since Y1 + Y1 = V V H and V H V=I substuting eq(15) into eq(13) and left-multiplying (13) by V H yiels the following matrix
Z= D -1 U H
Y2 V (17)
Note that Z is an M*M matrix and zi
are eigen values of this matrix. So the GPOF method is finished as form
the matrix Y1 by the definitions given above. Then select number of
exponentials to be fit to the data (M) by using singular value decomposition
and then form the matrix Z and the eigen values gives us zi .
One more hint is that if L is chosen to be equal to M, then GPOF method is equivalent to least-square prony method.
I think at this point it will be very useful to introduce you two Matlab codes. One of them implements a modified version of the prony method while the other one implements the GPOF algorithm :
function [s,R]=gpof(y,Ts)
%GPOF MEthod.Ts represents the
sampling period
%N repseresnt number of samples
N=length(y);
L=fix(N/2);
for j=1:L+1
for i=1:N-L,
Y(i,j)=y(i+j-1);
end
end
Y1=Y(1:N-L-1,1:L+1);Y2=Y(2:N-L,1:L+1);
[u,D,v]=svd(Y1);
[m,n]=size(D);
% Determine the value of number of exponentials.
nd=min(m,n);
i=1;M=1;
sigmamax=D(1,1);sigmac=D(2,2);
while ((sigmac/sigmamax)>1e-3)&(i<nd)
i=i+1;
sigmac=D(i,i);
M=i-1;
end
invD=zeros(M,M);
for i=1:M,
invD(i,i)=1/D(i,i);
end
vp=v(1:n,1:M);up=u(1:m,1:M);
Z=invD*up'*Y2*vp;
z=eig(Z);
s=log(z)/Ts;
alfa=-real(s);
omega=imag(s);
Z=[];
for k=0:N-1,
Z=[Z;((z.').^k)];
end
%RESIDUES
R=Z\y.';
function [b,a,mu] = mprony(y,t,p,bstart);
%MPRONY Fits a sum of exponential functions to data by a modified Prony
% method.
%
% B = MPRONY(Y,T,P)
approximates Y(i) by a weighted sum of P
% exponentials sum_j=1^p A(j)*exp(B(j)*T(i)). The T(i) are
% assumed equally spaced. B and A may be complex, although the
% sum will be real if the data
are.
%
% Starting values for the B(i)
are optional supplied by
% MPRONY(Y,T,P,BSTART). The A(i) and the fitted values are
% optionally returned by
[B,A,MU] = MPRONY(Y,T,P,BSTART).
% References:
% Kahn, M., Mackisack, M. S.,
Osborne, M. R., and Smyth, G. K. (1992).
% On the consistency of Prony's method and related algorithms.
% J. Comput. Graph. Statist., 1, 329-349.
% Osborne, M. R., and Smyth,
G. K. (1995). A modified Prony algorithm
% for fitting sums of exponential functions. SIAM J. Sci. Statist.
% Comput., 16, 119-138.
% Gordon Smyth, U of
Queensland, gks@maths.uq.oz.au
% 17 Dec 90. Latest revision 29 Sep 95.
[n cy]=size(y);
dt=t(2)-t(1);
% form Y
Y=zeros(n-p,p+1);
i=1:(n-p);
for j=1:p+1,
Y(:,j)=y(i+j-1);
end;
% starting values
if nargin < 4,
[x d]=eig(Y'*Y); [l
jmin]=min(diag(d)); c=x(:,jmin);
else
c=poly(exp(bstart*dt)); c=c(:);
c=c(p+1:-1:1)/norm(c);
end;
% form B
% X=zeros(n,n-p);
X=sparse( [],[],[],n,n-p,(n-p)*(p+1) );
for j=1:n-p,
X(j:j+p,j)=conj(c);
end;
MY=(X'*X)\Y;
v=MY*c;
V=zeros(n,p+1);
for j=1:p+1,
V(j:n-p+j-1,j)=v;
end;
B=( Y'*MY-V'*V )./(n-p);
% initial eigenvalues
lold=inf;
[x d]=eig(B); [l jmin]=min(diag(d)); c=x(:,jmin);
lfirst=l;
tol=10^(-15+log(n));
iter=0;
while (abs((l-lold)/lfirst) > 1e-5) & (rcond(B) > tol) &
(iter<40);
iter=iter+1;
if iter==40;
disp('MProny. Max iterations reached.');
end;
% form B
for j=1:n-p,
X(j:j+p,j)=conj(c);
end;
MY=(X'*X)\Y;
v=MY*c;
V=zeros(n,p+1);
for j=1:p+1,
V(j:n-p+j-1,j)=v;
end;
B=( Y'*MY-V'*V )./(n-p);
% inverse iteration
lold=l;
[x d]=eig(B); [l
jmin]=min(diag(d)); c=x(:,jmin);
end;
% extract rate constants
b=log(roots( c(p+1:-1:1) ))/dt;
if nargout > 1,
A=exp(t*b');
a=A\y;
mu=A*a;
end;
EXAMPLE RUNS OF THE PROGRAM:
Example 1:
Function: cos(x)+ cos(2*x)+ cos(4*x)+ cos(8*x)
Sampling Range: [0,10]
Number of Samples:101
Method: GPOF
Outputs:
***Complex Poles***
S[0] = 0.0 -j8.0
S[1] = 0.0 +j8.0
S[2] = 0.0 -j4.0
S[3] = 0.0 -j2.0
S[4] = 0.0 -j1.0
S[5] = 0.0 +j4.0
S[6] = 0.0 +j1.0
S[7] = 0.0 +j2.0
***Complex Residues***
R[0] = 0.5 +j0.0
R[1] = 0.5 +j0.0
R[2] = 0.5 +j0.0
R[3] = 0.5 +j0.0
R[4] = 0.5 +j0.0
R[5] = 0.5 +j0.0
R[6] = 0.5 +j0.0
R[7] = 0.5 +j0.0
Example2:
Function: cos(x)+ cos(2*x)+ cos(4*x)+ cos(8*x)
Sampling Range: [0,10]
Number of Samples:101
Method:Prony
No of Exponentials:11
Outputs:
***Complex Poles***
S[0] = -16.623266 -j18.084541
S[1] = -16.623266 +j18.084541
S[2] = -29.461227 -j31.415926
S[3] = 0.0 -j8.0
S[4] = 0.0 +j8.0
S[5] = 0.0 -j4.0
S[6] = 0.0 -j2.0
S[7] = 0.0 -j1.0
S[8] = 0.0 +j1.0
S[9] = 0.0 +j2.0
S[10] = 0.0 +j4.0
***Complex Residues***
R[0] = 0.0 +j0.0
R[1] = 0.0 +j0.0
R[2] = 0.0 +j0.0
R[3] = 0.5 +j0.0
R[4] = 0.5 +j0.0
R[5] = 0.5 +j0.0
R[6] = 0.5 +j0.0
R[7] = 0.5 +j0.0
R[8] = 0.5 +j0.0
R[9] = 0.5 +j0.0
R[10] = 0.5 +j0.0
Example3:
Function:sin(x)+ sin(3*x)+ sin(7*x)
Sampling Range: [0,10]
Number of Samples:101
Method:Prony
No of Exponentials:7
Outputs:
***Complex Poles***
S[0] = -1.2558355 +j31.415926
S[1] = 0.0 +j7.0
S[2] = 0.0 +j3.0
S[3] = 0.0 +j1.0
S[4] = 0.0 -j1.0
S[5] = 0.0 -j3.0
S[6] = 0.0 -j7.0
***Complex Residues***
R[0] = 0.0 +j0.0
R[1] = 0.0 -j0.5
R[2] = 0.0 -j0.5
R[3] = 0.0 -j0.5
R[4] = 0.0 +j0.5
R[5] = 0.0 +j0.5
R[6] = 0.0 +j0.5
Example4:
Function:sin(x)+ sin(3*x)+ sin(7*x)
Sampling Range: [0,10]
Number of Samples:101
Method:GPOF
Outputs:
***Complex
Poles***
S[0] = 0.0 -j7.0
S[1] = 0.0 +j7.0
S[2] = 0.0 -j3.0
S[3] = 0.0 -j1.0
S[4] = 0.0 +j1.0
S[5] = 0.0 +j3.0
***Complex Residues***
R[0] = 0.0 +j0.5
R[1] = 0.0 -j0.5
R[2] = 0.0 +j0.5
R[3] = 0.0 +j0.5
R[4] = 0.0 -j0.5
R[5] = 0.0 -j0.5
Example5:
Function:sin(x)+ cos(3*x)+ sin(9*x)
Sampling Range: [0,10]
Number of Samples:101
Method:GPOF
Outputs:
***Complex Poles***
S[0] = 0.0 +j9.0
S[1] = 0.0 -j9.0
S[2] = 0.0 +j3.0
S[3] = 0.0 +j1.0
S[4] = 0.0 -j1.0
S[5] = 0.0 -j3.0
***Complex Residues***
R[0] = 0.0 -j0.5
R[1] = 0.0 +j0.5
R[2] = 0.5 +j0.0
R[3] = 0.0 -j0.5
R[4] = 0.0 +j0.5
R[5] = 0.5 +j0.0
Example6:
Function:sin(x)+ cos(3*x)+ sin(9*x)
Sampling Range: [0,10]
Number of Samples:101
Method:Prony
Number of Exponentials:6
Outputs:
***Complex Poles***
S[0] = 0.0 -j9.0
S[1] = 0.0 -j3.0
S[2] = 0.0 -j1.0
S[3] = 0.0 +j1.0
S[4] = 0.0 +j3.0
S[5] = 0.0 +j9.0
***Complex
Residues***
R[0] = 0.0 +j0.5
R[1] = 0.5 +j0.0
R[2] = 0.0 +j0.5
R[3] = 0.0 -j0.5
R[4] = 0.5 +j0.0
R[5] = 0.0 -j0.5
Example7:
Function:exp(jx)
Samples:
1
2
3
43
5
6
7
8
9
10
Sampling Period: 1
Method:GPOF
Outputs:
***Complex
Poles***
S[0] =
-0.20412043 -j3.7232028E-17
S[1] = -1.031164
+j1.5920029
S[2] = -1.031164
-j1.5920029
***Complex Residues***
R[0] = 26.65605
+j0.0
R[1] = -11.704902
+j32.226086
R[2] = -11.704902
-j32.226086
As seen from the
examples the results are quite reasonable. Advantages and disadvantages of
using Prony’s Method or GPOF are generally known and discussed so its upto the
user to decide which of them to use.