Subsections

• 1 Propagation
• 2 Fourier transform with a lens
• 3 Optical signal processing
• 4 More optical signal processing

Experiment 6: Propagation and optical signal processing

1 Propagation

In this part of the experiment, you will investigate the propagation of an optical field to the far field. The input optical field will be generated by illuminating a periodic pattern of squares with a plane wave. This field will propagate to the far field where its Fourier transform will be visible.

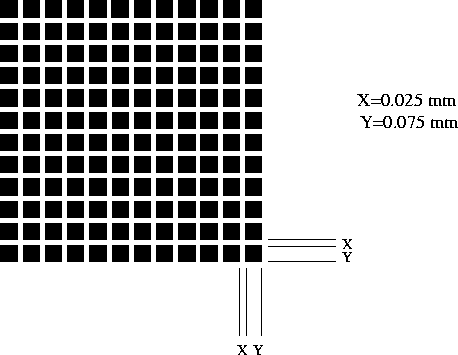
Calculate the far field intensity distribution for the pattern shown in the figure. Assume a unity amplitude where there is a dark square and zero amplitude elsewhere. The pattern can be mathematically represented as a properly scaled rectangle function multiplied by an array of smaller rectangle functions as

$$t(x,y) = f(x)f(y)$$

$$f(x) = \mbox{rect} \left[ \frac{x}{12(X+Y)} \right] \sum_{q=... ...infty} \mbox{rect} \left[ \frac{x-(q-1/2)(X+Y)}{Y} \right] .$$

In addition, calculate the distance for which Fraunhofer approximation begins to hold.

Expand the laser beam with a Galilean telescope ($f=-25$ mm and $f= 100$ mm). Make sure that it is well collimated. Mount the pattern on a slide holder and position it at the center of the beam. The central portion of the Gaussian beam approximates a plane wave. Observe the intensity of the field as it propagates after the pattern. Describe how the intensity distribution changes as the field propagates. Observe the intensity distribution in the far field. Compare this distribution (quantitatively) with your calculations.

2 Fourier transform with a lens

Position the $f=50$ mm lens at a distance of one focal length from the signal plane (optical pattern). The best way to do this is to move the lens back and forth and obtain a sharp image of the pattern on the wall. Examine the light distribution at the Fourier plane, one focal length from the lens. (The exact location of the Fourier plane is where the light distribution is sharpest.) This is a scaled down version of the same distribution you saw in the far field. Verify this visually.

3 Optical signal processing

In this part of the experiment, you will set up an optical signal processing system. You will take the Fourier transform of an input signal using a lens, filter the transform by placing various filters at the Fourier plane, and take the inverse transform.

It is possible to take the inverse transform by placing another $f=50$ mm lens at a distance of one focal length from the Fourier plane, thus setting up a 4-$f$ system. However, this will produce an output signal that is difficult to inspect with the naked eye. Instead, you can let the light distribution at the Fourier plane propagate to the far field, as in the previous part, thus taking the inverse transform. Observe that the output signal is a scaled up version of the input signal when there is no filter in the Fourier plane.

In all of the steps below, draw space domain and frequency domain diagrams to explain the filtering process. Mount a slide holder onto the XZ translation stage such that different filters can be positioned accurately at the Fourier plane. Position the 0.5 mm slit in the Fourier plane at the center of the light distribution. What type of filter is this? What is the effect of the filter on the output signal? Replace with the 0.2 mm slit and compare. Rotate the filter by 90$^{\circ}$ and compare. Using your results from part 1, calculate the fundamental spatial frequency of the periodic variation of the input signal. Which one of the apertures filters out this frequency component?

Position the 0.5 mm circular aperture at the center of the transform. What type of filter is this? What is the effect of the filter on the output signal?

Position the 0.25 mm opaque point at the center of the transform. What type of filter is this? What is the effect of the filter on the output signal? Replace with the 0.5 mm point and compare.

4 More optical signal processing

In this part, the assistant will demonstrate spatial filtering of various input fields with the same filters used in the previous part.

The laser beam will be expanded with a Galilean telescope ($f=-25$ mm and $f=300$ mm). An object slide will be placed after the collimating lens. A $f= 100$ mm lens will be positioned at a distance of one focal length from the signal plane. Examine the light distribution at the Fourier plane, one focal length from the lens. Observe that the far field intensity is a scaled up version of the object intensity when there is no filter in the Fourier plane. The assistant will place various filters in the image plane (on a translation stage). Note the changes in the output.