The spatial characteristics of a laser beam are determined by the laser resonator (see Chapters 9 and 14). Most lasers have spherical mirror Fabry-Perot resonators that have Hermite-Gaussian spatial modes. Usually, only the lowest order transverse resonator mode oscillates, resulting in a Gaussian output beam. The location and the radius of the beam waist depend on the laser resonator. For the He-Ne lasers used in the Optics Laboratory, you can assume that the beam waist is located at the output aperture of the laser. The diameter of the beam waist is approximately 0.48 mm.
Some applications require a laser beam with low divergence (small
2![]() ). This can be achieved by expanding a laser beam with a
telescope so that
). This can be achieved by expanding a laser beam with a
telescope so that ![]() and
and ![]() become large, resulting in a
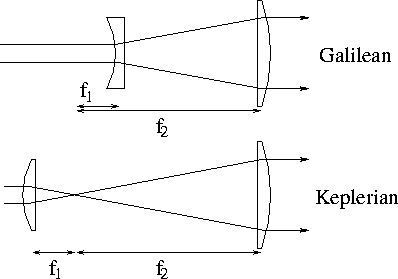
collimated beam. A Galilean or a Keplerian telescope may be used for
this purpose. In both telescopes, the first lens (
become large, resulting in a
collimated beam. A Galilean or a Keplerian telescope may be used for
this purpose. In both telescopes, the first lens (![]() ) expands the
beam and the second lens (
) expands the
beam and the second lens (![]() ) recollimates it.
) recollimates it.
Some applications require a beam that is focused to a small spot. A single positive lens may be adequate for this purpose. The spot size decreases with increasing beam radius at the focusing lens.
First expand the laser beam with a Galilean telescope (![]() mm and
mm and
![]() mm). Make sure that the resulting beam is well collimated by
visually checking that the beam propagates virtually without
divergence after the second lens.
mm). Make sure that the resulting beam is well collimated by
visually checking that the beam propagates virtually without
divergence after the second lens.
Mount the 0.5 mm aperture (one of the light source apertures) on a slide holder. Mount the slide holder onto the translation stage such that the aperture can be positioned anywhere on the transverse plane. Position the translation stage on the optical bench so that the aperture is in the beam path, and visually center the aperture on the beam. Position the optical power meter after the aperture. Screw the He-Ne (red) filter in front of the power meter detector. Make sure that all the light going through the aperture is incident on the detector at each measurement point.
Measure the intensity at 1 mm intervals along the horizontal
transverse direction. Plot your data and try to fit a Gaussian curve
to it. Determine the beam radius ![]() from your graph. Assuming that
the beam waist is located right after the recollimating lens,
calculate the beam radius at 100 m, 1 km, and 10 km. Calculate the
divergence angle (
from your graph. Assuming that
the beam waist is located right after the recollimating lens,
calculate the beam radius at 100 m, 1 km, and 10 km. Calculate the
divergence angle (![]() ) of this beam. Using the known
magnification of the telescope (
) of this beam. Using the known
magnification of the telescope (![]() ), calculate the
approximate beam radius and divergence before the telescope.
), calculate the
approximate beam radius and divergence before the telescope.
In this experiment you will measure the beam radius for a diverging
beam at two positions along the direction of propagation and deduce
all the beam parameters from these measurements. Before coming to the
laboratory, derive all necessary expressions to deduce ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() , and
, and ![]() from a knowledge of
from a knowledge of ![]() ,
,
![]() , and
, and ![]() . Note that you do not know the values of
. Note that you do not know the values of
![]() and
and ![]() , but only their difference
, but only their difference ![]() .
.
In the laboratory, focus the laser beam with a ![]() mm lens. Using
the 0.5 mm aperture and the translation stage, measure the beam
radius at two different
mm lens. Using
the 0.5 mm aperture and the translation stage, measure the beam
radius at two different ![]() positions
positions ![]() and
and ![]() after the focus.
(To measure the beam radus, just find the location where the intensity
drops down to
after the focus.
(To measure the beam radus, just find the location where the intensity
drops down to ![]() of its peak value rather than measuring the
entire beam profile.) Choose
of its peak value rather than measuring the
entire beam profile.) Choose ![]() and
and ![]() so that the beam is
considerably larger than the aperture (0.5 mm) you are using. From
your data, find
so that the beam is
considerably larger than the aperture (0.5 mm) you are using. From
your data, find ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and
![]() .
.