Subsections

• 1 Two wave interference
• 2 Double slit interference
• 3 Newton's rings

Experiment 3: Interference

For an interference pattern to be observable, the phase difference between the interfering waves must remain fairly constant in time. Light sources with good phase stability are said to be coherent. In amplitude-splitting interferometers, the two interfering waves are obtained by partial reflection and transmission of the same wave. These waves are usually delayed with respect to each other at the point of interference. Their phase difference remains constant in time if the light source is temporally coherent. Coherence time is the longest time delay for which the waves still show interference. In wavefront-splitting interferometers, the two interfering waves are obtained from different spatial regions of the same original wavefront. Their phase difference remains constant in time if the light source is spatially coherent. Coherence length is the longest distance on the wavefront for which the waves still interfere.

The fringe visibility (or fringe contrast) is defined as

$$V=\frac{I_{\mbox{max\vphantom{i}}}-I_{\mbox{min}}} {I_{\mbox{max\vphantom{i}}}+I_{\mbox{min}}}$$

where $I_{\mbox{max\vphantom{i}}}$ and $I_{\mbox{min}}$ are the maximum and minimum values of intensity in Equation (2.5-4). For two coherent waves of equal intensity, the fringe visibility is unity. If the waves have different intensities but are still coherent, the fringe visibility can be calculated from Equation (2.5-4). If the waves are partially coherent but have the same intensity, the fringe visibility becomes a measure of the degree of coherence.

1 Two wave interference

The interference of two monochromatic plane waves propagating at an angle to each other results in a periodic modulation of intensity in space. This modulation can be observed as interference fringes on a screen. If the screen is placed perpendicular to the propagation direction of one of the beams, the fringe separation (modulation period) is given by $\Delta x=\lambda_0/\sin\theta$ where $\theta$ is the angle between the two plane waves (See Equation (2.5-7)).

Reflections from the front and back surfaces of a glass plate with a small wedge angle propagate in slightly different directions as shown in the figure. A screen placed on the beam path shows interference fringes. (For small angles of incidence, the intensity of the two beams are approximately equal; therefore, the fringe visibility is high.) This configuration is an example of an amplitude-splitting interferometer.

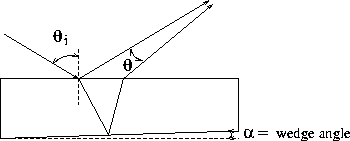
Derive an expression that relates the resulting fringe separation $\Delta x$ to the wedge angle of the glass plate $\alpha$. (It is safe to assume that $\alpha$ is very small.) Find the wedge angle of the glass plate from a measurement of the fringe separation. To do this, expand the laser beam with a Galilean telescope ($f=-25$ mm and $f=400$ mm). Position the glass plate on the angle measurement rotation base, as far from the laser as possible. Adjust the angle of incidence so that a number of fringes are visible on the reflected beam. To measure the fringe separation $\Delta x$ accurately, count the number of fringes over a distance and divide this measured distance to the number of fringes.

2 Double slit interference

The double slit experiment of Thomas Young is one of the most famous experiments in the history of optics. Young's experiment unequivocally established the wave nature of light by demonstrating interference between two light waves.

The double slit experiment is also based on two wave interference. It is an example of a wavefront-splitting interferometer. Therefore, the fringe visibility is a measure of spatial coherence.

Expand the laser beam with a Galilean telescope ($f=-25$ mm and $f=200$ mm). Mount the component with double slits in a slide holder and position it in the path of the beam. Select the 40 $\mu$m wide and 250 $\mu$m spaced pair of slits with the aperture mask. (The aperture mask should be placed right before the slits so that it has a sharp shadow.) View the interference pattern on a piece of paper, far from the slits. Slide the aperture mask horizontally to block one of the slits and observe the interference pattern disappear. Illuminate both slits again. Measure the fringe separation at a distance from the slits. From this measurement, calculate the slit spacing using Equation (2.5-8) and compare this with the given value. Repeat these measurements for the 40 $\mu$m wide and 500 $\mu$m spaced pair of slits.

Repeat the same experiment with the incandescent light source. Position the slits far from the light source so that the spatial coherence is high. (More on this in Chapter 10.) Use the diffuser as a screen; look from the opposite side towards the light source. Move the light source closer to the slits and observe the drop in fringe visibility. Why do you think the visibility is a function of light source distance from the slits?

3 Newton's rings

When a spherical surface is brought in contact with a flat surface, surface reflections result in concentric interference fringes. The point of contact is a dark fringe if both surfaces are clean. Derive an expression for the radius of the $m$th dark fringe for a given wavelength $\lambda_0$ ( $\lambda_0\ll R$). In the laboratory, your assistant will demonstrate Newton's rings with a $\lambda_0 = 546$ nm light source.